윌콕슨 순위합 검정(Wilcoxon Rank Sum test)은 기본적으로 (one/two)sample 간의 차이를 비교하고자 할 때, 평균(mean) 대신 중위수(median)를 사용한 비모수 검정이다. 이와 대비되는 모수적 방법은 잘 알려진 Student T-test이다.
우선 모수검정과 비모수검정에대 내용을 간단히 정리하면 다음과 같다.
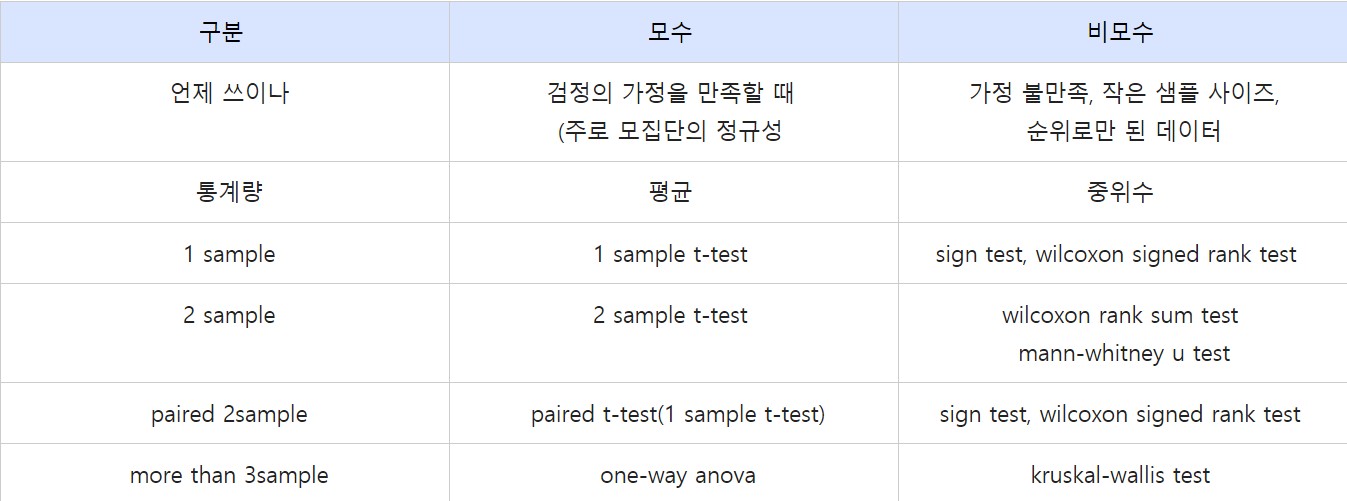
표에서 제시한 바와 같이 윌콕슨 검정은 맨-휘트니 검정(Mann-Whitney test)과 비슷한 역할을 수행하며 표본이 정규분포를 따르지 않는다고 가정한다.
한편 통계툴 R의 wilcox.test를 활용해 2개의 사례를 통해 윌콕슨 검점에 대해 좀 더 이해하도록 하자. 한 사례는 독립 1-표본 검정이고 다른 한 사례는 독립 2-표본 검정을 실시한 것인데, 모두 올랑더&울프(1973)의 저서<비모수 통계방법론="">에 수록된 데이터들이다.
1-표본 검정:
자료는 해밀턴 우울 척도를 이용하여 총 9명 우울증 환자에게 신경안정제 투약전(x)과 투약후(y) 간의 효과를 비교한 것이다.
x <- c(1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)
wilcox.test(x, y, paired = TRUE, alternative = "greater")
wilcox.test(y - x, alternative = "less") # The same.
Wilcoxon signed rank test
data: x and y
V = 40, p-value = 0.01953
alternative hypothesis: true location shift is greater than 0
P-value가 0.01953로서 유의수준 5%에서 귀무가설(H0: 별 두 집단 간에 차이는 없다)을 기각하게 되어 두 집단이 차이가 있는 것으로 판단된다.
2-표본 검정:
x <- c(0.80, 0.83, 1.89, 1.04, 1.45, 1.38, 1.91, 1.64, 0.73, 1.46)
y <- c(1.15, 0.88, 0.90, 0.74, 1.21)
wilcox.test(x, y, alternative = "g") # greater
Wilcoxon rank sum test
data: x and y
W = 35, p-value = 0.1272
alternative hypothesis: true location shift is greater than 0
P-value가 0.1272로서 유의수준 10%에서 귀무가설(H0: 별 두 집단 간에 효과 차이는 없다)을 채택하게 되며, 즉 차이가 없는 것으로 확인할 수 있다.